 |
| Ronald Graham and his wife Fan Chung |
"The Mathemagician"
Ronald Graham is not one of those "high IQ, low EQ" mathematicians that you are familiar with. He is the only one of its kind, and the people tend to call him " The Mathemagician". Literally... Believe it or not, he is "a highly skilled trampolinist and juggler", and the past president of the International Jugglers' Association. In fact, he was even on stage with Cirque du Soleil (recently visited Istanbul for a set of shows) and in an issue of Discover magazine about the Science of the Circus.
Recently a professor in the Computer Science Department of UCSD(University of California at San Diego), Prof. Graham considered a problem in Ramsey theory, and gave a "large number " as an upperbound for its solution. Since then, this number, known as Graham's number, became well known as the largest number ever used in a mathematical proof. It was so large when compared with the largest numbers previously used in mathematics that, people had tough times in perceiving it.Well actually, they still do.Perhaps the most ironic thing about this number was, it was an upper bound solution to a problem to which most of people would give the trivial answer: 6. Isn't it quite hilarious that we cannot even calculate how many times Graham's number is bigger than 6 today?
Graham's Number
 |
| Ronald Graham while juggling |
Recently a professor in the Computer Science Department of UCSD(University of California at San Diego), Prof. Graham considered a problem in Ramsey theory, and gave a "large number " as an upperbound for its solution. Since then, this number, known as Graham's number, became well known as the largest number ever used in a mathematical proof. It was so large when compared with the largest numbers previously used in mathematics that, people had tough times in perceiving it.Well actually, they still do.Perhaps the most ironic thing about this number was, it was an upper bound solution to a problem to which most of people would give the trivial answer: 6. Isn't it quite hilarious that we cannot even calculate how many times Graham's number is bigger than 6 today?
Graham's Number
Graham's number is connected to the following problem in the branch of mathematics known as Ramsey Theory:
- Consider an n-dimensional hypercube, and connect each pair of vertices to obtain a complete graph on 2n vertices. Then colour each of the edges of this graph either red or blue.
- What is the smallest value of n for which every such colouring contains at least one single-coloured 4-vertex planar complete subgraph?
where the number of arrows in each layer, starting at the top layer, is specified by the value of the next layer below it; that is,
So to explain better we can say that g(1)= 3^^^^3 meaning basically 3^27. For g(2), there will be g(1) number of arrors between 3s, that is to say g(2)= 3^^^^.....^^^3, where the number of ^'s is g(1) and so on until g(64) , which is the Graham's number itself.
It comes as a no surprise to say that this is an unbelievably huge number, so huge that if we could write each number of the Graham's number on every atom in the observable universe, it would not be enough. As a result:
1.We will never learn how many digits it has.
2. We will never learn the first digit of the Graham's number
3.We will never learn if there are more 1s than 0s in Graham's number
Well, we will pretty much never learn anything. Why am I so confident? Can't a modern computer in the future store the Graham's number? The entire number is far too big to be stored in perfect precision by any computer that has ever existed or ever will exist. How can I say "ever will exist"? Because, even written in scientific notation, i.e. with only one digit of precision, the number of digits in the exponent would exceed the number of atoms in the observable universe. The total number is easily larger than the number of Planck volumes into which the observable universe can be divided. If the whole observable universe were a computer, and every tiny quark and neutrino represented a bit of data, it could not store the entire number in absolute precision.
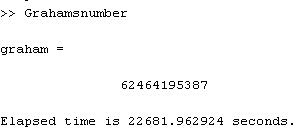
The only thing we can do about the Graham's number is that we are able to calculate the last digits of it by using the "modular exponentiation" technique. In fact, I implemented this technique in a Matlab code ( you can download it HERE), and I was able to calculate the last 11 digits of the Graham's number in , well, 6 hours. Either I need a better computer or I should quit writing programs so inefficient :)

The link to the MATLAB code doesn't work. Could you possibly post it in the MATLAB File Exchange (http://www.mathworks.com/matlabcentral/fileexchange/)?
ReplyDeleteCurious . . . what significance are the 3 and 64 in Graham's number?
ReplyDeleteAfter all I could arbitrarily name a number N,
such that N = n1048576,
where n1 = 7↑↑↑↑↑↑↑↑7 and nk = 7↑(nk-1)7
Obviously N, although still infinitely short of ∞, would be mind-bogglingly larger than G . . . no?
The Graham's number is a number that has been used in some serious mathematical proof. What you have said has no reference to any mathematical sum and you can keep increasing or decreasing any value of a number that way till infinity.
DeletePossible the first digit of grahams number is 4.
ReplyDelete