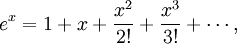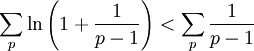Infinitude of prime numbers: Euclid, Euler and the mathematical beauty

Euclid with his students

   

Euclid, as depicted above, used to love teaching and sharing his knowledge with others, and made this teaching process one of his daily routines. One day, a youth who had just begun to learn geometry with Euclid, when he had learnt the first proposition, inquired, "What do I get by learning these things?" So Euclid called a slave and said "Give him three pence, since he must make a gain out of what he learns." 

Euclid's answer probably summarizes why there are still people today, who are really not earning a lot , engaging in pure mathematics and spending their lifetime on a subject which will only be understood by a small portion of the human population on earth. Euclid, who is generally referred as the "Father of Geometry" was probably one of the scientists who enjoyed what he was doing the most. Therefore, it probably comes as no surprise that , he established one of the most elegant proofs in the math history- if not the most elegant one.

Euclid's proof

Are prime numbers infinite? Perhaps one of the most interesting things about the infinitude of prime numbers is that, nobody who is not interested in mathematics very much seemed to have a correct/reasonable answer about it. I usually get answers like "Hmmm,I don't know" from people when I asked about this. We can confidently say that the answer for this question is not intuitive, that is to say, it is not related with our everyday experiences nor observations.

When Euclid asked himself this question, and sought for an answer, he found out that the answer was very simple. A summary can be seen below.

Suppose that p₁=2 < p₂ = 3 < ... < p_r are all of the primes. Let P = p₁p₂...p_r+1 and let p be a prime dividing P; then p can not be any of p₁, p₂, ..., p_r, otherwise p would divide the difference P-p₁p₂...p_r=1, which is impossible. So this prime p is still another prime, and p₁, p₂, ..., p_r would not be all of the primes.

Roughly speaking, as you might have already understood, suppose that the number of prime numbers are finite, and let the last prime number be p_r   .So now if you multiplied all the prime numbers including p_r  and just add 1 to it, you would get another prime number, which contradicts with the first assumption. Hence, prime numbers are infinite.

Not only me, but also lots of mathematicians agree that this is one of the most elegant and beautiful proofs in the math history. The fact that it is so simple and can even be understood by a primary school student makes you want to think : "That's it!".

Euler's proof

Leonhard Euler depicted on a 1983 stamp from the German Democratic Republic. The stamp also includes a diagram of an icosahedron and Euler's famous polyhedral formula 

The underlying idea of Euler's proof is very different than that of Euclid's. In fact,although more complicated,his proof is stronger and makes use of analytical methods. In essence, he proves that the sum of the reciprocals of the primes is infinite.  I can't say I am a big fan of Euler because of his intrigues against Daniel Bernoulli, which he conducted with Daniel's father. But anyways, you know what they say: “Render unto Caesar the things which are Caesar’s”.

 

He used the following equality between the regular harmonic series and the infinite products called "Euler products". In the right hand side, p refers to the prime numbers.Euler noted that if there were only a finite number of primes, then the product on the right would clearly converge, contradicting the divergence of the harmonic series. This is a direct result of the fundamental theorem of arithmetic. If you are not convinced, please see: "On the infinitude of prime numbers" by Shailesh A Shirali pg. 9-11.

                                    

Then, Euler took the natural logarithm of both sides and by using the properties of logarithm function he found:

                  

Since

we get e^x > 1 + x and x > ln(1 + x).

So;

Hence diverges. (Because we know the left side diverges as it is equal to the natural logarithm of the sum of the  harmonic series.)But 1/(p_i − 1) < 1/p_i−1 where p_i is the i^th prime. Hence 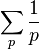diverges.

This directly implies that , there are infinite number of prime numbers(otherwise the sum would converge).Perhaps none of you could guess a simple divergence test, which you probably learned in Calculus courses, would be the main element of such a beautiful proof.

Mathematical Beauty

Mathematicians usually describe a proof as elegant, when it is simple,unusually succinct, derives a result in a surprising way,is based on new and original insights and can be easily generalized to solve a family of similar problems. Probably one of the main requirements the mathematicians are defending to understand the mathematical beauty is that ,well, "you have to be a mathematician".
 

In his book, "Art of Mathematics", Jerry King draws a figure as depicted above to summarize the  aesthetic view of different people about mathematics.The people in the inner circle (like myself)are people very close to mathematics because they use it day by day, are the ES types (the engineers and scientists). Most engineers and scientists appreciate mathematics solely and only because of its utility. 

The point outside the two concentric circles, point P, represents people who don't care about mathematics. (including most non-science and non-math teachers) These “P people” are unfortunately in the majority.

And according to King, you could only see the beauty of mathematics if you are in the gray zone. That is, if you are a mathematician :) Well a bit arrogant, but who can oppose it ?

Graham's Number and Infinity

Ronald Graham and his wife Fan Chung

What is the biggest number that you know of? Centillion, googol,googolplex? A googol is 10¹⁰⁰  and  a googolplex is  10^Googol  , which is already an unbelievably large number. Of course you can go on forever, by taking the powers of these numbers until you reach the infinity. But what is the largest number that is "useful" for mathematics? The answer is the mysterious Graham's number. Graham's number is so ridiculously huge that  it trumps googolplex by a long shot.

"The Mathemagician"

Ronald Graham is not one of those "high IQ, low EQ" mathematicians that you are familiar with. He is the only one of its kind, and the people tend to call him " The Mathemagician". Literally... Believe it or not, he is "a highly skilled trampolinist and juggler", and the past president of the International Jugglers' Association. In fact, he was even on stage with Cirque du Soleil (recently visited Istanbul for a set of shows) and in an issue of Discover magazine about the Science of the Circus.

Ronald Graham while juggling

Recently a professor in  the Computer Science Department of UCSD(University of California at San Diego), Prof. Graham considered a problem in Ramsey theory, and gave a "large number " as an upperbound for its solution. Since then, this number, known as Graham's number, became well known as the largest number ever used in a mathematical proof. It was so large when compared with the largest numbers previously used in mathematics that, people had tough times in perceiving it.Well actually, they still do.Perhaps the most ironic thing about this number was, it was an upper bound solution to a problem to which most of people would give the trivial answer: 6. Isn't it quite hilarious that we cannot even calculate how many times Graham's number is bigger than 6 today?


Graham's Number

Graham's number is connected to the following problem in the branch of mathematics known as Ramsey Theory:

Consider an n-dimensional hypercube, and connect each pair of vertices to obtain a complete graph on 2ⁿ vertices. Then colour each of the edges of this graph either red or blue.

What is the smallest value of n for which every such colouring contains at least one single-coloured 4-vertex planar complete subgraph?

Well , this may sound quite complicated and I do not want to bore you with details, so let's proceed with what Graham's number really is.

where the number of arrows in each layer, starting at the top layer, is specified by the value of the next layer below it; that is,

So to explain better we can say that g(1)= 3^^^^3 meaning basically 3^27. For g(2), there will be g(1) number of arrors between 3s, that is to say g(2)= 3^^^^.....^^^3, where the number of ^'s is g(1) and so on until g(64) , which is the Graham's number itself.

It comes as a no surprise to say that this is an unbelievably huge number, so huge that if we could write each number of the Graham's number on every atom in the observable universe, it would not be enough.  As a result:

1.We will never learn how many digits it has.

2. We will never learn the first digit of the Graham's number

3.We will never learn if there are more 1s than 0s in Graham's number

Well, we will pretty much never learn anything.  Why am I so confident? Can't a modern computer in the future store the Graham's number? The entire number is far too big to be stored in perfect precision by any computer that has ever existed or ever will exist. How can I say "ever will exist"? Because, even written in scientific notation, i.e. with only one digit of precision, the number of digits in the exponent would exceed the number of atoms in the observable universe. The total number is easily larger than the number of Planck volumes into which the observable universe can be divided. If the whole observable universe were a computer, and every tiny quark and neutrino represented a bit of data, it could not store the entire number in absolute precision.

The only thing we can do about the Graham's number is that we are able to calculate the last digits of it by using the "modular exponentiation" technique. In fact, I implemented this technique in a Matlab code ( you can download it HERE), and I was able to calculate the last 11 digits of the Graham's number in , well, 6 hours. Either I need a better computer or I should quit writing programs so inefficient :)

It is obvious that the size of Graham's number is beyond our perception. But the ironic thing is, you, me and Ronald Graham is  exactly at the same distance with infinity: Infinity